=
45o ao redor do eixo referencial cartesiano x
para que P1' esteja no plano xy.
Executar o mesmo deslocamento para P1 e P2.
Última Atualização 24/ 9/ 2014
A animação na figura acima representa a rotação do vértice P2 do cubo com coordenadas cartesianas 5; 10; 10 ao redor da diagonal do cubo, em vermelho e definida pelos vértices P0(5; 0; 0) e P1(-5; 10; 10). A trajetória do ponto P2 é representada por uma sequência regular de discos coloridos, projetados do início até completar 120o. As coordenadas cartesianas ao longo de x, y e z para os vértices do cubo estão listadas em azul no lado esquerdo da figura.
Porém o método matemático para que o computador efetue a rotação executa 8 passos, conforme explicado no texto que segue.
Considere o seguinte
x, y, z = Referencial Cartesiano com origem em o.
P0, P1 = dois pontos que definem o eixo de rotação e este eixo coincide com a diagonal do cubo.
P2 = ponto a ser girado de 120o.
Tabela-1.Coordenadas iniciais
| Ponto | x | y | z |
| P0 | 5 | 0 | 0 |
| P1 | -5 | 10 | 10 |
| P2 | 5 | 10 | 10 |
Passo-1. Aplicar ao ponto P0 o deslocamento
-5x; 0y; 0z para ele coincidir com a origem.
Executar o mesmo deslocamento para P1
e P2.
Tabela-2.Coordenadas após o passo-1.
| Ponto | x | y | z |
| P0' | 0 | 0 | 0 |
| P1' | -10 | 10 | 10 |
| P2' | 0 | 10 | 10 |
Passo-2. Girar =
45o ao redor do eixo referencial cartesiano x
para que P1' esteja no plano xy.
Executar o mesmo deslocamento para P1
e P2.
Utilizar a matriz rotação
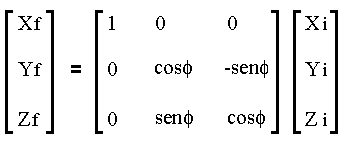
Tabela-3.Coordenadas obtidas após o passo-2.
| Ponto | x | y | z |
| P0'' | 0 | 0 | 0 |
| P1'' | -10 | 0 | 10 * (21/2) |
| P2'' | 0 | 0 | 10 * (21/2) |
Passo-3. Calcular o ângulo de rotação do segmento oP1'' para que o ponto P1'' alcance o eixo referencial z .
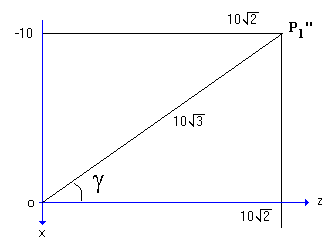
Passo-4. Girar o ponto P1''
e o ponto P2'' de 
=
35,264o ao redor do eixo referencial y.
Utilizar a matriz rotação
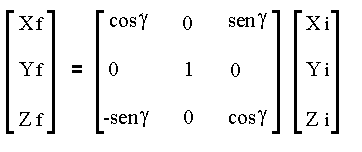
Tabela-4.Coordenadas obtidas após o passo-4.
| Ponto | x | y | z |
| P0''' | 0 | 0 | 0 |
| P1''' | 0 | 0 | 17,321 |
| P2''' | 8,1650 | 0 | 11,547 |
Passo-5. Executar a rotação escolhida:
girar de 
= 120o
o ponto P2''' ao redor do eixo
referencial z.
Utilizar a matriz rotação
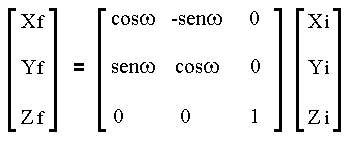
Tabela-5. Coordenadas do ponto P2iv obtidas após
o passo-5.
| Ponto | x | y | z |
| P2iv | -4,0825 | 7,0711 | 11,547 |
Passo-6. Reverter: girar de -35,264o o ponto P2iv ao redor de y.
Tabela-6. Coordenadas do ponto P2v obtidas após
o passo-6.
| Ponto | x | y | z |
| P2v | -9,9999 | 7,0711 | 7,0711 |
Passo-7. Reverter: girar o ponto P2v de -45o ao redor de x.
Tabela-7. Coordenadas do ponto P2vi obtidas após
o passo-7.
| Ponto | x | y | z |
| P2vi | -10 | 10 | 0 |
Passo-8. Reverter: deslocar o ponto P2vi de +5x; 0y; 0z para a posição final.
Tabela-8. Coordenadas do ponto P2vii obtidas após
o passo-8.
Rotação completada.
| Ponto | x | y | z |
| P2vii | -5 | 10 | 0 |
Conclusão
O ponto P2vii coincide com o ponto P3.
Observação
O programa que projeta a figura animada foi realizado com o auxílio do programa Rotação de Objetos ao Redor de um Eixo Arbitrário
Exercício
Utilizar o recurso citado acima para obter as coordenadas cartesianas finais para o ponto P2 ( 5; 10; 10) após a rotação inicial de 120o e após uma rotação de -120o e após uma rotação de 240o ao redor do mesmo eixo definido pelos pontos P0 (5; 0; 0) e P1 (-5; 10; 10). Escreva as tuas conclusões. Sugestão: utilize x[0] = 5; y[0] = 10; z[0] = 10 e x[1] = 5; y[1] = 10; z[1] = 10 porque o programa do recurso demanda pelo menos dois pontos para definir um segmento, neste caso o segmento tem comprimento xero.
Referência
Fundamentals of Crystallography, Edited by C. GIACOVAZZO, Second Edition, Oxford University Press, Great Britain, 2002.
Por favor, envie teus comentários.
Tabela de temas.