Método do Pó, Difração de Raios-x
Convida-se a utilizar o método de Hanavalt¹ para identificar os componentes de uma amostra mediante o difratograma da figura, em azul. Ao mover o mouse sobre um pico do difratograma da amostra será mostrado o ângulo de difração  em azul e a intensidade relativa I/I', nesta simulação I = altura do pico e ruído I' = 1.

A tabela-A mostra o número de cada raio difratado entre colchetes em ordem decrescente de intensidade relativa I/I' e a distância d em Angstrom (1 A=10^-10 m) entre planos cristalográficos "ricos em átomos"² na amostra³. Para ver outras seções da tabela-A será preciso arrastar o mouse sobre o quadrado verde.
Raios-x com comprimento de onda igual a 1,5418 Angstrom⁴ foram usados nesta simulação.
A tabela-B mostra seis distâncias d como definido acima em ordem decrescente de intensidade relativa I/I' para cada padrão⁵, respectivamente em cada linha da página 1. Se um dos 10 padrões na página tem distâncias d combinantes com a amostra, um clique na linha mudará a cor da linha de cinza para vermelho e apresentará o conjunto completo de distâncias d  do padrão selecionado na tabela-C organizada como na tabela-A e desenhará também o difratograma do padrão em preto. Ao mover o mouse sobre um pico do difratograma do padrão será mostrado o ângulo de difração  em preto e a intensidade relativa I/I'. Um clique sobre o botão V mostrará a página seguinte, até a página 11. Para voltar à página anterior será preciso clicar no botão com V invertido. Se não existir um padrão combinante com a amostra numa página será necessário procurar em outra página da tabela-B.
Um novo acesso a esta página Análise de Uma Miustura de Minerais - Simulação vai apresentar uma amostra com outra mistura de minerais diferentes.

O simulador desta página considera cada padrão como um material puro em cristais perfeitos e cada amostra como uma mistura de 2 padrões puros, cada um com cristais perfeitos. Isto explica porque os difratogramas aqui simulados têm picos em forma de simples segmentos de retas de uma dimensão, isto não ocorre na natureza mineral do planeta Terra.

A figura abaixo é uma imagem estática do simulador.

Exercícios
1) Escreva a fórmulas químicas e nomes dos minerais presentes na amostra, respectivamente.
2) Qual é o metal do anodo de uma fonte de raios-x com comprimento de onda 1,5418 Angstrom?
3) Qual é o metal no filtro usado para raios-x com comprimento de onda 1,5418 Angstrom?
4) Qual é a voltagem de aceleração de elétrons necessária para obter raios-x com comprimento de onda 1,5418 Angstrom?

Referências
1. HANAWALT, J. D,. Manual Search/Match Methods for Powder Diffraction in 1986, Powder Diffraction, Vol 1, Issue 1, March 1986.
2. BRAGG, W.H.and BRAGG, W.L., The Reflection of x-rays by crystals, Proc. R. Soc. Lond., A 88 (605), 428-38, 1913.
3. AZAROFF, L.V. and BUERGER, M.J., The Powder Method in X-ray Christallography, McGraw-Hill, New York, 1958.
4. STOUT, G.H. and JENSEN, L.H., X-ray Structure Determination, Macmillan, London, 1968.
5. BERRY, L.G.(Editor), Selected Powder Diffraction Data for Minerals, Joint Commitee on Powder Difftraction Standards, Philadelphia, 1974

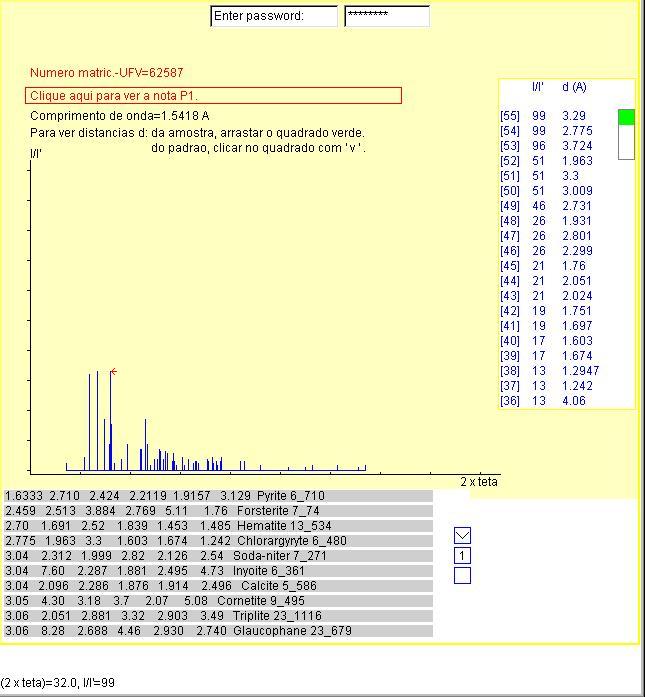
Tabela de temas
 

Apresentação